Variation d'un rectangle dans un cercle

Travail dirigé
 | Jeudi 15 Janvier 2026

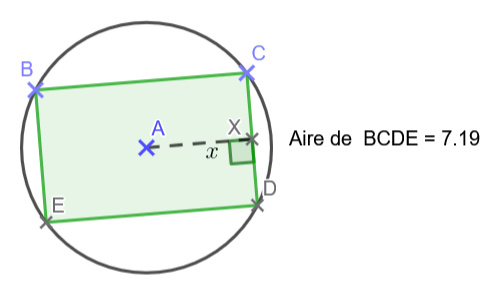
Considérons un rectangle \( BCDE \), inscrit dans un cercle de centre \( A \) et de rayon \( r \).

Sur la figure, on a fixé \( r=2 \).

1. Géométriquement
  1. Construire cette figure avec précision sur GeoGebra pour \( r = 2 \).
  2. Quelle est l'aire maximale atteinte ?
  3. Que remarque-t-on ?
2. Modélisation
  1. Exprimer la longeur \( BC \) du rectangle en fonction de \( x \).
  2. Exprimer la largeur \( CD \) du rectangle en fonction de \( r \) et \( x \).
  3. En déduire l'expression de l'aire du rectangle.

3. Analyse du problème

Considérons la fonction \( f \) définie par :

\( \displaystyle f(x) = 4x\sqrt{4 - x^2} \)

Il s'agit de l'aire du rectangle pour \( r = 2 \).
  1. Quel est son ensemble de définition ?
  2. Tracer la représentation graphique de la fonction sur GeoGebra.
  3. Quel semble être son maximum ?
  4. Comparer le résultat obtenu avec la question 1..