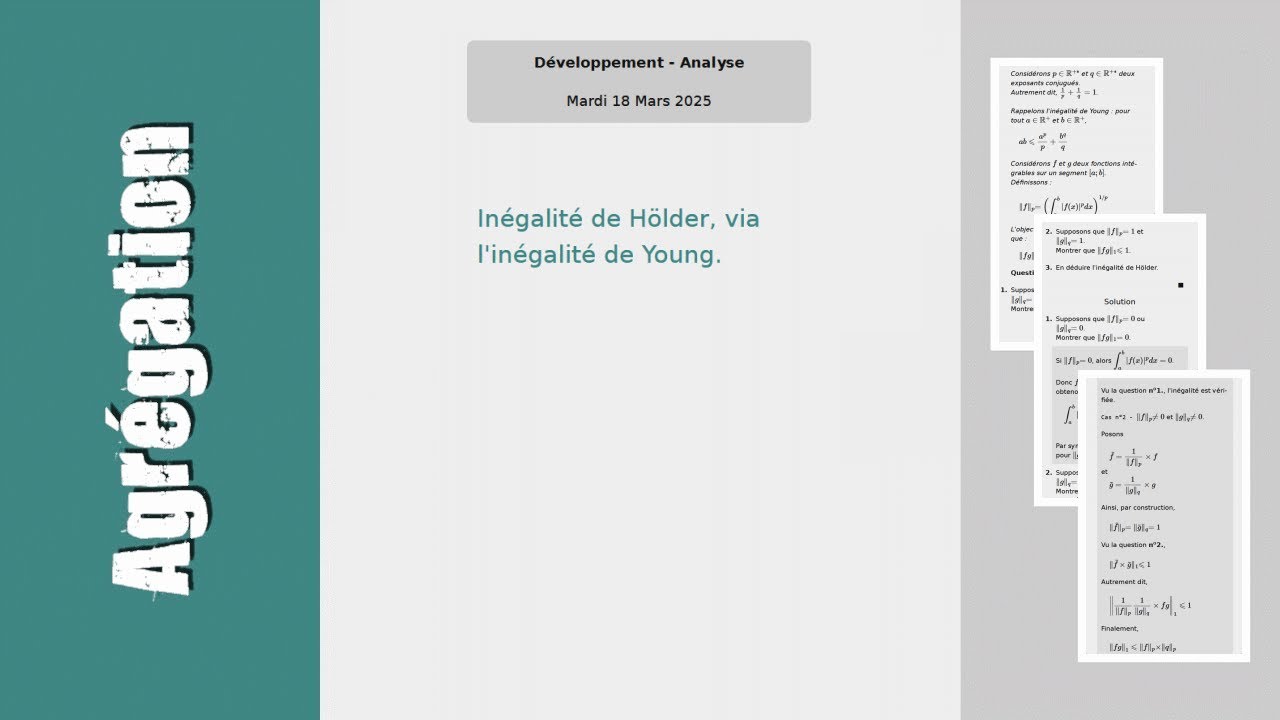
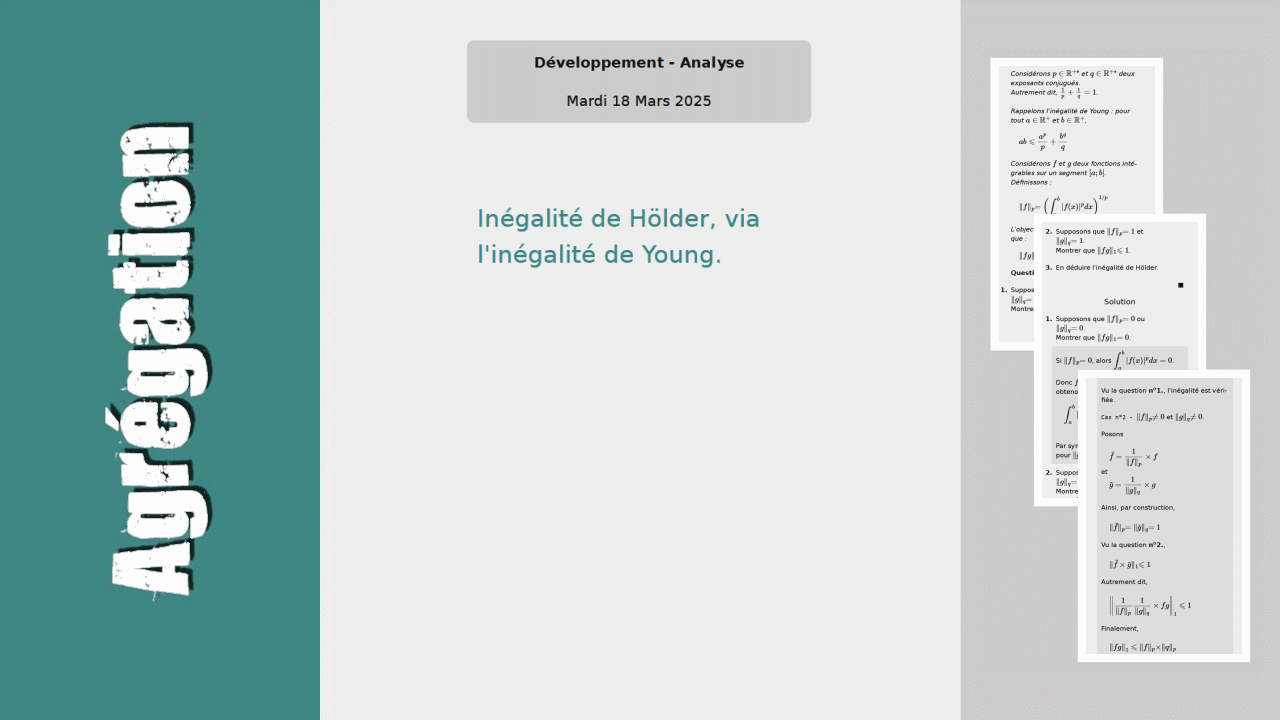
Considérons \( p\in{\mathbb R}^{+*} \) et \( q\in{\mathbb R}^{+*} \) deux exposants conjugués.
Autrement dit, \( \frac{1}{p} + \frac{1}{q} = 1 \).

Rappelons l'inégalité de Young : pour tout \( a \in{\mathbb R}^+ \) et \( b\in{\mathbb R}^+ \),

\( ab\leqslant\dfrac{a^p}{p} + \dfrac{b^q}{q} \)

Considérons \( f \) et \( g \) deux fonctions intégrables sur un segment \( [a; b] \).
Définissons :

\( \displaystyle \lVert f\lVert_p = \left(\int_a^b |f(x)|^p dx \right)^{1/p} \)

L'objectif de l'exercice est de montrer que :

\( \lVert fg\lVert_1 \leqslant \lVert f\lVert_p \times \lVert g\lVert_q \)

Questions

1. Supposons que \( \lVert f\lVert_p = 0 \) ou \( \lVert g\lVert_q = 0 \). Montrer que \( \lVert fg\lVert_1 = 0 \).

2. Supposons que \( \lVert f\lVert_p = 1 \) et \( \lVert g\lVert_q = 1 \). Montrer que \( \lVert fg\lVert_1 \leqslant1 \).

3. En déduire l'inégalité de Hölder.

■

Solution

1. Supposons que \( \lVert f\lVert_p = 0 \) ou \( \lVert g\lVert_q = 0 \). Montrer que \( \lVert fg\lVert_1 = 0 \).

Si \( \lVert f\lVert_p = 0 \), alors \( \displaystyle\int_a^b |f(x)|^p dx = 0 \).

Donc \( f = 0 \) presque partout, et nous obtenons :

\( \displaystyle\int_a^b |f(x)g(x)| dx = \int_a^b 0\times|g(x)| dx \) \( = 0 \)

Par symétrie, le résultat est identique pour \( \lVert g\lVert_q = 0 \).

2. Supposons que \( \lVert f\lVert_p = 1 \) et \( \lVert g\lVert_q = 1 \). Montrer que \( \lVert fg\lVert_1 \leqslant1 \).

D'après l'inégalité de Young, pour tout \( x\in[a; b] \) :

\( |f(x)g(x)|\leqslant \dfrac{|f(x)|^p}{p} + \dfrac{|g(x)|^q}{q} \)

En intégrant termes à termes :

\( \displaystyle\int_a^b |f(x)g(x)| dx \leqslant \) \( \displaystyle\int_a^b \dfrac{|f(x)|^p}{p} dx + \int_a^b \dfrac{|g(x)|^q}{q} dx \)

Autrement dit,

\( \lVert fg\lVert_1 \leqslant \dfrac{\left\lVert f\right\lVert_p^p}{p} + \dfrac{\left\lVert g\right\lVert_q^q}{q} \)

\( \lVert fg\lVert_1 \leqslant \dfrac{1}{p} + \dfrac{1}{q} \)

Finalement, \( \lVert fg\lVert_1 \leqslant 1 \).

3. En déduire l'inégalité de Hölder.

Cas n°1 - \( \lVert f\lVert_p = 0 \) ou \( \lVert g\lVert_q = 0 \).

Vu la question n^o1., l'inégalité est vérifiée.

Cas n°2 - \( \lVert f\lVert_p \neq 0 \) et \( \lVert g\lVert_q \neq 0 \).

Posons   \( \tilde{f} = \dfrac{1}{\lVert f\lVert_p} \times f \) et \( \tilde{g} = \dfrac{1}{\lVert g\lVert_q} \times g \) .

Ainsi, par construction,   \( \lVert \tilde{f}\lVert_p = \lVert \tilde{g}\lVert_q = 1 \) .

Vu la question n^o2.,   \( \lVert \tilde{f}\times \tilde{g}\lVert_1 \leqslant 1 \) .

Autrement dit,   \( \left\lVert \dfrac{1}{\lVert f\lVert_p} \dfrac{1}{\lVert g\lVert_q} \times fg\right\lVert_1 \leqslant 1 \) .

Finalement,   \( \left\lVert fg\right\lVert_1 \leqslant \lVert f\lVert_p \times \lVert q\lVert_p \) .