Inégalité de Young généralisée.

Fixons $ M\in{\mathbb R}^{+*} $.

Soit $ f : [0; M] \rightarrow {\mathbb R} $ continue strictement croissante telle que $ f(0) = 0 $.

Ainsi, $ Im f = [0; f(M)] $.

De plus, d'après le théorème des fonctions réciproques, $ f $ admet une fonction réciproque $ f^{-1} : [0; f(M)] \rightarrow [0; M] $ continue et strictement croissante.

L'objectif de l'exercice est la démonstration du :

Théorème [Inégalité de Young Généralisée]
Pour tout $ a\in [0; M] $ et $ b\in[0; f(M)] $,

$ \displaystyle ab\leqslant \int_0^a f(x)dx + \displaystyle\int_0^b f^{-1}(y)dy $

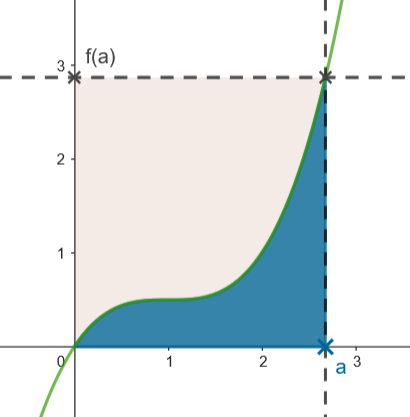
L'idée de cette inégalité vient du lien entre les courbes représentatives d'une fonction inversible et de sa fonction réciproque : les surfaces, par symétrie, s'emboitent parfaitement pour recréer l'aire du rectangle $ a \times f(a) $.

1. Démontrer que pour tout $ a\in [0; M] $,

$ \displaystyle a f(a) = \int_0^a f(x)dx $$ \displaystyle + \int_0^{f(a)} f^{-1}(y)dy $

$ \displaystyle S_n = \sum_{k=0}^{n-1} (x_{k+1} - x_k) $$ \displaystyle \times\frac{ (f(x_{k+1}) + f(x_k)) }{2} $

$ \displaystyle $\lim_{n\rightarrow +\infty} S_n = \int_0^a f(x)dx$ $

$ \displaystyle T_n = \sum_{k=0}^{n-1} (y_{k+1} - y_k) $$ \displaystyle \times\frac{ (f^{-1}(y_{k+1}) + f^{-1}(y_k)) }{2} $

$ \displaystyle \phantom{T_n} =\sum_{k=0}^{n-1} (f(x_{k+1}) - f(x_k)) $$ \displaystyle \times\frac{(x_{k+1} + x_k) }{2} $

$ \displaystyle \lim_{n\rightarrow +\infty} T_n = \int_0^{f(a)} f^{-1}(y)dy $

$ \displaystyle S_n + T_n =\sum_{k=0}^{n-1} $$ \displaystyle \small\frac{ (x_{k+1} - x_k)\times (f(x_{k+1}) + f(x_k))}{2} $$ \displaystyle + \small\frac{(f(x_{k+1}) - f(x_k))\times (x_{k+1} + x_k) }{2} $

$ \displaystyle S_n + T_n =\sum_{k=0}^{n-1} {\small x_{k+1} f(x_{k+1}) - x_k f(x_k)} $

$ \displaystyle S_n + T_n = x_{n} f(x_{n}) - x_0 f(x_0) $

$ \displaystyle S_n + T_n = a f(a) $

$ \displaystyle \lim_{n\rightarrow +\infty} S_n + T_n = \lim_{n\rightarrow +\infty}S_n $$ \displaystyle + \lim_{n\rightarrow +\infty}T_n $

$ \displaystyle a f(a) = \int_0^a f(x)dx $$ \displaystyle + \displaystyle\int_0^{f(a)} f^{-1}(y)dy $

2. En déduire que pour tout $ a\in [0; M] $ et $ b\in[0; f(M)] $,

$ \displaystyle ab \leqslant \int_0^a f(x)dx + \displaystyle\int_0^b f^{-1}(y)dy $

$ \displaystyle \int_0^a f(x)dx + \displaystyle\int_0^b f^{-1}(y)dy $$ \displaystyle = \int_0^a f(x)dx + \displaystyle\int_0^{f(a)} f^{-1}(y)dy $$ \displaystyle + \int_{f(a)}^b f^{-1}(y)dy $

$ \displaystyle \int_0^a f(x)dx + \displaystyle\int_0^b f^{-1}(y)dy $$ \displaystyle = af(a) + \int_{f(a)}^b f^{-1}(y)dy $

$ \displaystyle \int_{f(a)}^b f^{-1}(y)dy > f^{-1}(f(a))\times {\small (b-f(a))} $

$ \displaystyle \int_{f(a)}^b f^{-1}(y)dy = - \int_b^{f(a)} f^{-1}(y)dy $$ \displaystyle > f^{-1}(f(a))\times {\small (b-f(a))} $

3. Démontrer que l'égalité est obtenue si et seulement si $ b = f(a) $.

Considérons $ p\in{\mathbb R}^{+*} $ et $ q\in{\mathbb R}^{+*} $ deux exposants conjugués. Autrement dit, $ \frac{1}{p} + \frac{1}{q} = 1 $.

4. Montrer que pour tout $ a \in{\mathbb R}^+ $ et $ b\in{\mathbb R}^+ $,

$ ab \leqslant \dfrac{a^p}{p} + \dfrac{b^q}{q} $

■

Solution

1. Démontrer que pour tout $ a\in [0; M] $,

Soit $ n\in{\mathbb N}^* $. Utilisons la méthode des trapèzes pour approcher la surface de $ f $. Fixons $ \left\{x_0 = a, \dots, x_n = b\right\} $ une subdivision de $ [0; a] $ et posons :

Ainsi,

Faisons de même pour $ f^{-1} $, avec pour subdivisions $ \left\{y_k = f(x_k) ~|~ k\in \left[\!\left[ 1; n \right]\!\right] \right\} $, et posons :

Ainsi,

Maintenant, en sommant les expressions de $ S_n $ et $ T_n $ :

Développons et simplifions :

Par élimination télescopique :

Finalement, par passage à la limite :

2. En déduire que pour tout $ a\in [0; M] $ et $ b\in[0; f(M)] $,

La relation de Chasles donne :

Cas n°1 - Si $ f(a) < b $, $ f^{-1} $ étant strictement croissante et positive

Cas n°2 - Si $ f(a) > b $,

Donc, dans tous les cas,

$ \displaystyle\int_0^a f(x)dx + \int_0^b f^{-1}(y)dy $ $ > \underbrace{af(a) + a\times (b-f(a))}_{=ab} $

3. Démontrer que l'égalité est obtenue si et seulement si $ b = f(a) $.

Si $ b = f(a) $, l'égalité vient de la question 1..

Réciproquement, si nous avons l'égalité, la preuve de la question 2. par disjonction de cas montre les inégalités sont strictes. Le seul cas possible est alors $ f(a) = $b$ . $

4. Montrer que pour tout $ a \in{\mathbb R}^+ $ et $ b\in{\mathbb R}^+ $,

$ ab \leqslant \dfrac{a^p}{p} + \dfrac{b^q}{q} $

Considérons la fonction $ f : {\mathbb R}^+ \rightarrow {\mathbb R}^+ $ définie par $ f(x) = x^{p-1} $.

Elle est continue, strictement croissante, et $ f(0)=0 $.

Sa fonction réciproque est définie sur $ {\mathbb R}^+ $ par $ f^{-1}(y) = y^{\frac{1}{p-1}} = y^{q-1} $

Appliquons l'inégalité de Young Généralisée :

$ \displaystyle ab \leqslant \int_0^a x^{p-1} dx + \int_0^b y^{q-1} dy $

$ \displaystyle ab \leqslant \left[\dfrac{x^p}{p}\right]_0^a + \left[\dfrac{y^q}{q}\right]_0^b $

$ \displaystyle ab \leqslant\dfrac{a^p}{p} + \dfrac{b^q}{q} $