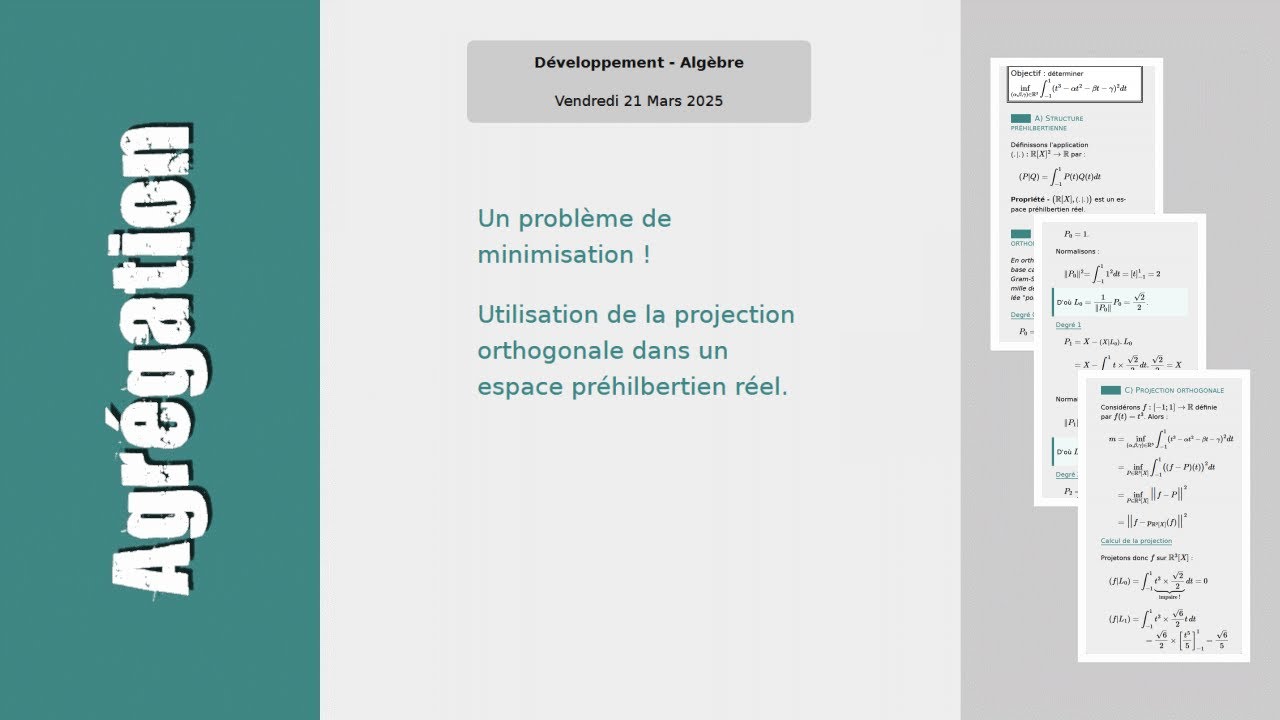
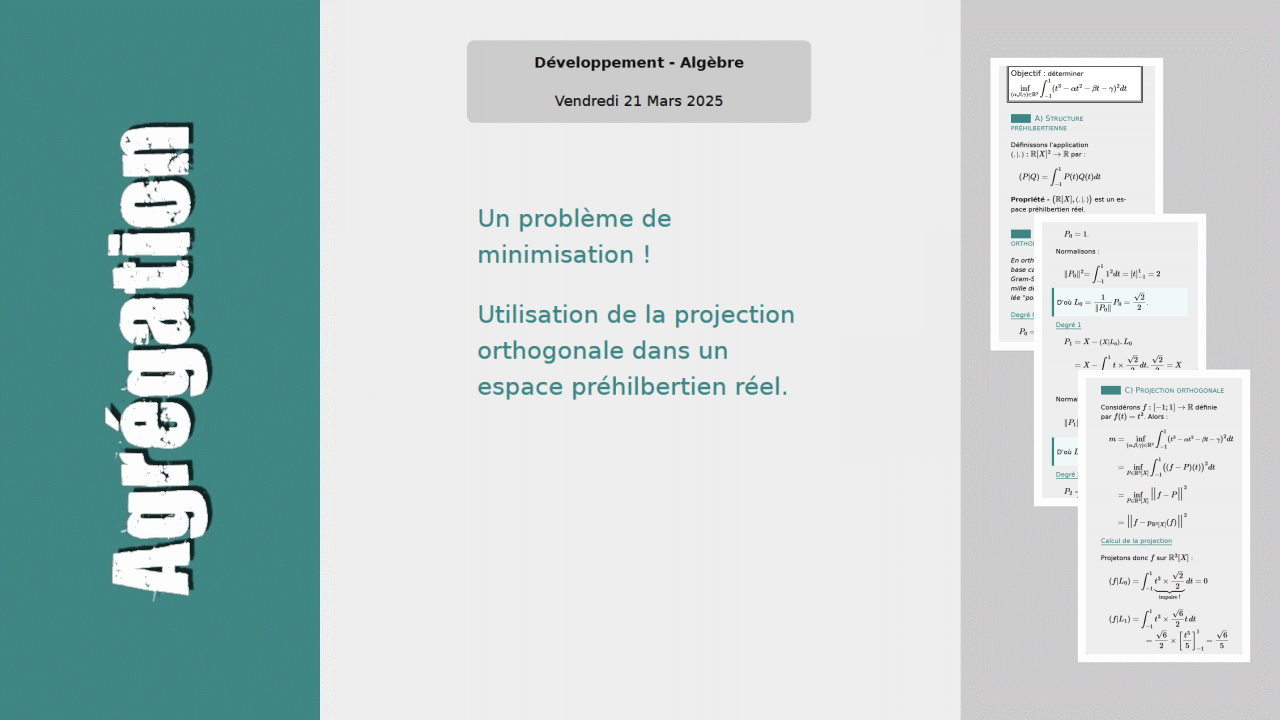
Objectif : déterminer \( \displaystyle\inf_{(\alpha, \beta, \gamma)\in{\mathbb R}^3}\int_{-1}^1 (t^3 - \alpha t^2 - \beta t - \gamma)^2 dt \)

A) Structure préhilbertienne

Définissons l'application \( {\small (.|.)} : {\mathbb R}[X]^2\rightarrow{\mathbb R} \) par :

\( (P|Q) = \displaystyle\int_{-1}^1 P(t)Q(t)dt \)

Propriété - \( \big({\mathbb R}[X], {\small (.|.)}\big) \) est un espace préhilbertien réel.

B) Construction d'une base orthonormée

En orthogonalisant les vecteurs de la base canonique par l'algorithme de Gram-Schmidt, nous obtenons une famille de polnômes orthonormaux appelée "polynômes de Legendre".

Degré 0

\( P_0 = 1 \).

Normalisons :

\( \displaystyle \lVert P_0\lVert ^2 = \int_{-1}^1 1^2 dt = \left[ t\right]_{-1}^1 = 2 \)

D'où \( L_0 = \dfrac{1}{\lVert P_0\lVert }P_0 = \dfrac{\sqrt{2}}{2} \).

Degré 1

\( \displaystyle P_1 = X - {\small(X|L_0)}.L_0 \)

\( \displaystyle \phantom{P_1} = X - \underbrace{\int_{-1}^1 t\times \dfrac{\sqrt{2}}{2} dt}_{\text{=0 car impaire}} . \dfrac{\sqrt{2}}{2} = X \)

Normalisons :

\( \lVert P_1\lVert ^2 = \displaystyle\int_{-1}^1 t^2 dt = \displaystyle\left[ \dfrac{t^3}{3}\right]_{-1}^1 = \dfrac{2}{3} \)

D'où \( L_1 = \dfrac{1}{\lVert P_1\lVert }P_1 = \dfrac{\sqrt{6}}{2} X \).

Degré 2

\( P_2 = X^2 - {\small(X^2|L_1)}.L_1 - {\small(X^2|L_0)}.L_0 \)

\( \displaystyle \phantom{P_2} = X^2 - \underbrace{\int_{-1}^1 t^2\times \frac{\sqrt{6}}{2} t dt}_{\text{=0 car impaire}} . \frac{\sqrt{6}}{2} X \)\( \displaystyle - \int_{-1}^1 t^2\times \frac{\sqrt{2}}{2} dt . \frac{\sqrt{2}}{2} \)

\( \displaystyle \phantom{P_2} = X^2 - \frac{\sqrt{2}}{2} \left[ \frac{t^3}{3}\right]_{-1}^1 \times \dfrac{\sqrt{2}}{2} \)

\( \displaystyle \phantom{P_2} = X^2 - \frac{1}{3} \)

Normalisons :

\( \displaystyle \lVert P_2\lVert ^2 = \int_{-1}^1 \big(t^2 - \frac{1}{3}\big)^2\,dt \)

\( \displaystyle \phantom{\lVert P_2\lVert ^2} = \int_{-1}^1 t^4 - 2\,t^2\,\frac{1}{3} + \frac{1}{9}\,dt \)

\( \displaystyle \phantom{\lVert P_2\lVert ^2} = \left[ \frac{t^5}{5} - \frac{2t^3}{9} + \frac{1}{9}t\right]_{-1}^1 \)

\( \displaystyle \phantom{\lVert P_2\lVert ^2} = \frac{2}{5} - \frac{4}{9} + \frac{2}{9} = \frac{8}{45} \)

D'où \( L_2 = \dfrac{1}{\lVert P_2\lVert }P_2 = \dfrac{3\sqrt{10}}{4} X^2 - \dfrac{\sqrt{10}}{4} \).

C) Projection orthogonale

Considérons \( f: [-1; 1]\rightarrow{\mathbb R} \) définie par \( f(t) = t^3 \). Alors :

\( m = \displaystyle\inf_{(\alpha, \beta, \gamma)\in{\mathbb R}^3}\int_{-1}^1 ({\small t^3 - \alpha t^2 - \beta t - \gamma})^2 dt \)

\( \phantom{m} = \displaystyle\inf_{P\in {\mathbb R}^3[X]}\int_{-1}^1 \bigl((f - P)(t)\bigr)^2 dt \)

\( \phantom{m} = \displaystyle\inf_{P\in {\mathbb R}^3[X]} {\LARGE\lVert}f-P{\LARGE\lVert}^2 \)

\( \phantom{m} = {\LARGE\lVert}f-p_{{\mathbb R}^3[X]}(f){\LARGE\lVert}^2 \)

Calcul de la projection

Projetons donc \( f \) sur \( {\mathbb R}^3[X] \) :

\( (f|L_0) = \displaystyle\int_{-1}^1 \underbrace{t^3 \times\dfrac{\sqrt{2}}{2}}_{\text{impaire !}}\,dt = 0 \)

\( \displaystyle (f|L_1) = \int_{-1}^1 t^3\times\dfrac{\sqrt{6}}{2}t\,dt \)\( \displaystyle = \dfrac{\sqrt{6}}{2} \times\left[\dfrac{t^5}{5}\right]_{-1}^1 = \dfrac{\sqrt{6}}{5} \)

\( \displaystyle (f|L_2) = \int_{-1}^1 \underbrace{\small t^3\times\left(\dfrac{\sqrt{10}}{2}t^2 - \dfrac{\sqrt{10}}{3}\right)}_{\text{impaire !}}\,dt \)\( \displaystyle = 0 \)

Ainsi,

\( \displaystyle p_{{\mathbb R}^3[X]}(f) = \displaystyle\sum_{i=0}^2 (f|L_i)L_i \)\( \displaystyle = \dfrac{\sqrt{6}}{5}. \dfrac{\sqrt{6}}{2}X = \dfrac{3}{5}X \)

Calcul du minimum

Finalement,

\( m = {\LARGE\lVert} f-p_{{\mathbb R}^3[X]}(f) {\LARGE\lVert}^2 \)

\( \phantom{m} = \displaystyle\int_{-1}^1 \left(t^3 - \dfrac{3}{5}t\right)^2\,dt \)

\( \phantom{m} = \displaystyle\int_{-1}^1 \left(t^6 - 2t^3\times\dfrac{3}{5}t + \dfrac{9}{25}t^2\right)\,dt \)

\( \phantom{m} = \left[ \dfrac{t^7}{7} - \dfrac{6}{5}\times\dfrac{t^5}{5} + \dfrac{9}{25}\times\dfrac{t^3}{3}\right]_{-1}^1 \)

\( \phantom{m} = \dfrac{2}{7} - \dfrac{12}{25} + \dfrac{6}{25} = \dfrac{8}{175} \)

Conclusion !

Le minimum \( m = \dfrac{8}{175} \) est atteint pour le polynôme \( p_{{\mathbb R}^3[X]}(f) = \dfrac{3}{5}X \).