Dans tout ce qui suit, \( (X_n) \) désigne une suite de variables aléatoires réelles discrètes et indépendantes, définies sur un espace probabilisé \( (\Omega, P) \).

Supposons que tous les \( X_n \) suivent une loi de Bernouilli \( {\cal B}(p) \), où \( p\in[0; 1] \).
Elles admettent alors la même espérance \( p \), et le même écart-type \( \sqrt{p(1-p)} \).

Notons la somme : \( \displaystyle S_n = \sum_{i=1}^n X_i \).

Elle suit une loi binomiale \( {\cal B}(n, p) \) que nous allons essayer d'approcher.

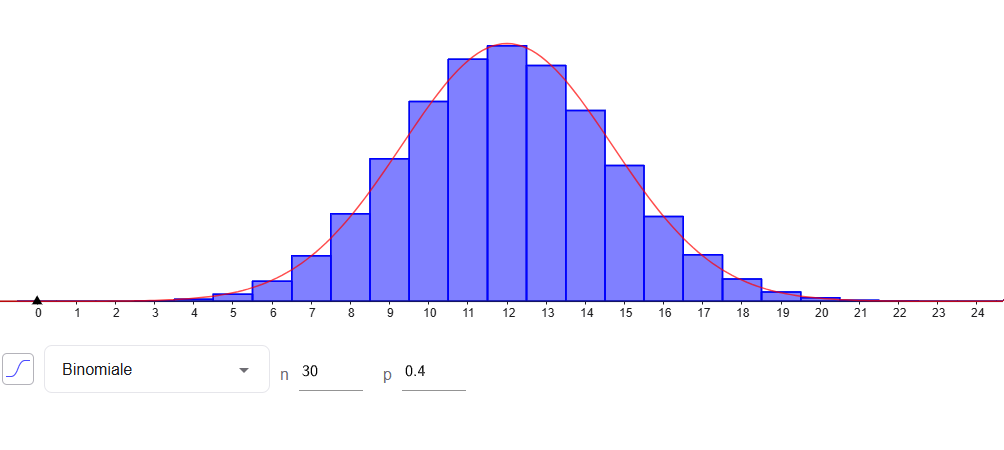
Notons la moyenne empirique :

\( \displaystyle \overline{X_n} = \frac{1}{n}S_n = \frac{1}{n}\sum_{i=1}^n X_i \)

Appliquons le théorème central de la limite. Pour tout \( x\in{\mathbb R} \) :

\( \displaystyle \lim_{n\rightarrow +\infty} P\left( \frac{\sqrt{n}}{\sqrt{p(1-p)}} \big(\overline{X_n} - p\big) \leq x\right) \)\( \displaystyle \,= \frac{1}{\sqrt{2\pi}}\int_{\small-\infty}^x {e^{-t^2 / 2}dt} \)

Finalement, en simplifiant, nous obtenons :

Théorème [De Moivre - Laplace] - Pour tout \( x\in\mathbb{R} \) :

\( \displaystyle \lim_{n\rightarrow +\infty} P\left( \frac{S_n - np}{\sqrt{np(1-p)}} \leq x\right) \)\( \displaystyle \,= \frac{1}{\sqrt{2\pi}}\int_{\small-\infty}^x {e^{-t^2 / 2}dt} \)

Application : en pratique, cette approximation de la loi binomiale est valable si \( n \) est suffisamment grand et si \( p \) n'est pas trop proche de 0 ou \( 1 \).

En général, on demande que \( np(1-p) \geqslant 10 \).