Dans tout ce qui suit, \( X \) désigne une variable aléatoire entière définie sur un espace probabilisé discret \( (\Omega, P) \).
On dit que \( X \) suit la loi géométrique de paramètre \( p\in[0; 1] \) si pour tout \( k\in\mathbb{N}^* \),
\( \displaystyle P(X = k) = (1-p)^{k-1} \times p \)
On note \( X \sim {\cal G}(p) \).
Espérance : \( E(X) = \dfrac{1}{p} \)
Variance : \( V(X) = \dfrac{1-p}{p^2} \)
1. Représentation sur GeoGebra
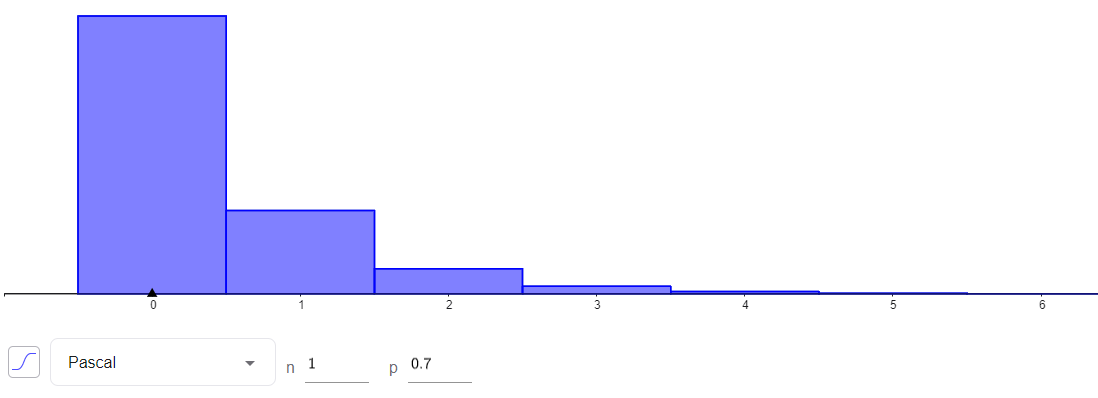
La loi géométrique peut-être vue comme un cas particulier d'une loi plus générale, appelée loi de Pascal.
2. Situation modélisée
Considérons une épreuve admettant deux issues : une réussite et un échec.
La loi géométrique modélise le nombre \( k \) de tentatives pour réussir l'épreuve - autrement dit une succession de \( k-1 \) échecs, suivie d'une réussite.
3. Fonction génératrice
Revenons à la définition :
\( \displaystyle G(t) = \displaystyle\sum_{k=1}^{+\infty} t^k P(X=k) \)
Appliquons cela dans le cas d'une loi géométrique :
\( \displaystyle G(t) = \displaystyle\sum_{k=1}^{+\infty} t^k (1-p)^{k-1} \times p \)
\( \displaystyle \phantom{G(t)} = tp\times \displaystyle\sum_{k=1}^{+\infty} (t\times(1-p))^{k-1} \)
On reconnait une série géométrique de raison \( t(1-p) \).
Elle converge si et seulement si \( \lvert t\times(1-p)\rvert \lt 1 \), c'est à dire :
\( \displaystyle t\in \left]-\dfrac{1}{1-p}; \dfrac{1}{1-p}\right[ \)
Finalement :
\( \displaystyle G(t) = tp\times \dfrac{1}{1 - t\times(1-p)} = \dfrac{tp}{1 - t + tp} \)
\( \displaystyle G'(t) = \small\dfrac{p(1 - t + tp) - tp(-1 +p)}{(1 - t + tp)^2} = \small\dfrac{p}{(1 - t + tp)^2} \)
\( \displaystyle G''(t) = \small\dfrac{-2p(-1+p)}{(1 - t + tp)^3} = \small\dfrac{p(2-2p)}{(1 - t + tp)^3} \)
4. Espérance et variance
Calcul de \( G'(1) \) et \( G''(1) \)
Notons que \( t=1 \) appartient au disque de convergence de \( G' \) et \( G'' \). Ainsi :
\( \displaystyle G'(1) = \small\dfrac{1}{p} \)
\( \displaystyle G''(1) = \small\dfrac{p(2-2p)}{p^3} = \small\dfrac{2-2p}{p^2} \)
Déterminons l'espérance
\( \displaystyle E(X) = G'(1) = \dfrac{1}{p} \)
Déterminons la variance
\( \displaystyle V(X) = G''(1) + G'(1) − G'(1)^2 \)
\( \displaystyle \phantom{V(X)} = \dfrac{2-2p}{p^2} + \dfrac{1}{p}- \dfrac{1}{p^2} \)
\( \displaystyle \phantom{V(X)} = \dfrac{2- 2p + p - 1}{p^2} \)
\( \displaystyle \phantom{V(X)} = \dfrac{1-p}{p^2} \)
