Dans tout ce qui suit, \( X \) désigne une variable aléatoire réelle discrète définie sur un espace probabilisé \( (\Omega, {\cal M}, P) \).
1. À retenir !
On dit que \( X \) suit la loi hypergéométrique de paramètres \( n\in \mathbb{N}^* \), \( p \in [0; 1] \) et \( N\in\mathbb{N} \) si pour tout \( k\in\left[\!\left[0, n\right]\!\right] \) :
\( P(X = k) = \dfrac{\displaystyle\binom{pN}{k}\times\binom{(1-p)N}{n-k}}{\displaystyle\binom{N}{n}} \)
où \( n \leq N \) et \( pN\in\mathbb{N} \).
On note \( X \sim {\cal H}(n, p, N) \).
Espérance : \( E(X) = np \)
Variance : \( V(X) = np(1-p)\dfrac{N-n}{N-1} \)
2. Situation modélisée
Considérons une population de \( N \) individus, dont \( pN \) présente un caractère particulier.
On en choisit \( n \) simulanément.
La loi hypergéométrique modélise le nombre \( k \) d'individus possédant ce caractère dans la sous-population de \( n \) individus.
Cette situation ressemble fortement à la loi binomiale !
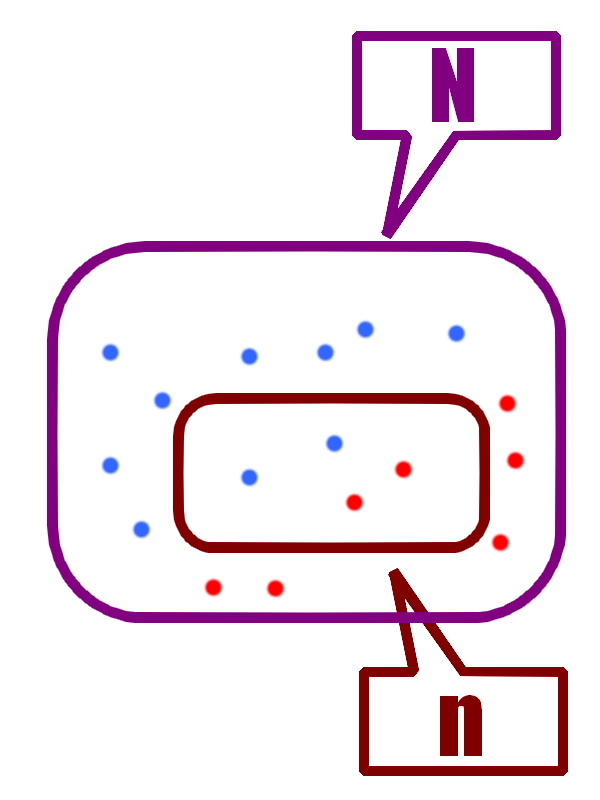
Plus précisemment, la loi binomiale modélise une situation avec remise, tandis que la loi hypergéométrique étudie un problème sans remise.
Ainsi, les résultats sont équivalents pour \( N \) grand et \( n \) petit. Mais lorsque \( n \) se rapproche trop de \( N \), les résultats deviennent significativement différents.
3. Fonction génératrice
Revenons à la définition :
\( \displaystyle G(t) = \displaystyle\sum_{k=0}^{n} t^k\,P(X=k) \)
Appliquons cela dans le cas d'une loi hypergéométrique :
\( \displaystyle G(t) = \displaystyle\sum_{k=0}^{n} t^k \frac{\displaystyle\binom{pN}{k}\times\binom{(1-p)N}{n-k}}{\displaystyle\binom{N}{n}} \)
Il n'y a pas de problème de convergence : il s'agit d'une somme finie !
Finalement :
\( \displaystyle G(t) = \dfrac{{\small\displaystyle \sum_{k=0}^{n}t^k}\binom{pN}{k}\binom{(1 - p) N}{n-k}}{\binom{N}{n}} \)
\( \displaystyle G'(t) = \dfrac{{\small\displaystyle\sum_{k=1}^{n}\,k t^{k-1}}\binom{pN}{k}\binom{(1-p)N}{n-k}}{\binom{N}{n}} \)
\( \displaystyle G''(t) = \dfrac{{\small\displaystyle\sum_{k=2}^{n}}{ (k-1) k t^{k-2}}\binom{pN}{k}\binom{(1-p)N}{n-k}}{\binom{N}{n}} \)
4. Espérance et variance
Calcul de \( G'(1) \)
\( \displaystyle G'(1) = \dfrac{{\small\displaystyle\sum_{k=1}^{n}\,k}\binom{pN}{k}\binom{(1-p)N}{n-k}}{\binom{N}{n}} \)
\( \displaystyle \phantom{G'(1)} = \dfrac{{\small\displaystyle\sum_{k=1}^{n}\,pN}\binom{pN - 1}{k- 1}\binom{(1-p)N}{n-k}}{\binom{N}{n}} \)
\( \displaystyle \phantom{G'(1)} = \dfrac{{\small pN\displaystyle\sum_{k=1}^{n}\,}\binom{pN - 1}{k- 1}\binom{(1-p)N}{n-k}}{\binom{N}{n}} \)
\( \displaystyle \phantom{G'(1)} = \dfrac{{\small pN\displaystyle\sum_{k=0}^{n-1}\,}\binom{pN - 1}{k}\binom{(1-p)N}{n-1-k}}{\binom{N}{n}} \)
On utilise alors la formule de Vandermonde :
\( \displaystyle G'(1) = \dfrac{{\small pN}\binom{pN - 1 + (1-p)N}{n-1}}{\binom{N}{n}} \)
Simplifions et colorons les binômes que l'on développe :
\( \displaystyle G'(1) = \small\dfrac{pN\color{green}\displaystyle\binom{N - 1}{n-1}}{\color{blue}\displaystyle\binom{N}{n}} \)
\( \displaystyle G'(1) = \small\dfrac{pN\color{blue}n! (N-n)!\color{green}(N - 1)!}{\color{blue}N!\color{green}(N - 1 -n+1)!(n-1)!} \)
Simplifions et colorons les facteurs qui s'éliminent :
\( \displaystyle G'(1) = \small\dfrac{p\color{brown}N\color{purple}n!\color{red}(N-n)!\color{brown}(N - 1)!}{\color{brown}N! \color{red}(N -n)!\color{purple}(n-1)!} = np \)
Calcul de \( G''(1) \)
Le calcul de \( G''(1) \) utilise exactement la même technique :
\( \displaystyle G''(1) = \dfrac{{\displaystyle\sum_{k=2}^{n}}{\small(k-1) k}\binom{pN}{k}\binom{(1-p)N}{n-k}}{\binom{N}{n}} \)
\( \displaystyle \phantom{G''(1)} = \dfrac{{\displaystyle\sum_{k=2}^{n}}{\small(k-1)pN}\binom{pN - 1}{k- 1}\binom{(1-p)N}{n-k}}{\binom{N}{n}} \)
\( \displaystyle \phantom{G''(1)} = \dfrac{{\small pN}{\displaystyle\sum_{k=2}^{n}}{\small(pN-1)}\binom{pN - 2}{k- 2}\binom{(1-p)N}{n-k}}{\binom{N}{n}} \)
\( \displaystyle \phantom{G''(1)} = \dfrac{{\small pN(pN-1)}{\displaystyle\sum_{k=2}^{n}}\,\binom{pN - 2}{k- 2}\binom{(1-p)N}{n-k}}{\binom{N}{n}} \)
\( \displaystyle \phantom{G''(1)} = \dfrac{{\small pN(pN-1)}{\displaystyle\sum_{k=0}^{n-2}}\,\binom{pN - 2}{k}\binom{(1-p)N}{n-2-k}}{\binom{N}{n}} \)
Utilisons alors la formule de Vandermonde :
\( \displaystyle G''(1) = \dfrac{{\small pN(pN-1)}\binom{pN - 2 + (1-p)N}{n-2}}{\binom{N}{n}} \)
Simplifions et colorons les binômes que l'on développe :
\( \displaystyle G''(1) = \small\dfrac{\displaystyle pN(pN-1)\color{green}\binom{N - 2}{n-2}}{\displaystyle \color{blue}\binom{N}{n}} \)
\( \displaystyle \phantom{G''(1)} = \small\dfrac{pN(pN-1) \color{green}(N-2)! \color{blue}n! (N-n)!}{\color{green}(n-2)! (N-2 - n+2)! \color{blue}N!} \)
Simplifions et colorons les facteurs qui s'éliminent :
\( \displaystyle G''(1) = \small\dfrac{p{\color{teal}N}(pN-1)\color{teal}(N-2)!\color{purple}n! \color{brown}(N-n)!}{\color{purple}(n-2)!\color{brown}(N - n)!\color{teal}N!} \)
\( \displaystyle \phantom{G''(1)} = \small\dfrac{p(pN-1)n(n-1)}{N-1} \)
Déterminons l'espérance
\( \displaystyle E(X) = G'(1) = np \)
Déterminons la variance
\( \displaystyle V(X) = G''(1) + G'(1) - G'(1)^2 \)
\( \displaystyle \phantom{V(X)} = \small \dfrac{p(pN-1)n(n-1)}{N-1} + np -(np)^2 \)
\( \displaystyle \phantom{V(X)} = \small np\left(\dfrac{(pN-1)(n-1)}{N-1} + 1 - pn\right) \)
\( \displaystyle \phantom{V(X)} = \small np\left(\dfrac{pNn - pN -n+1 }{N-1}\right. \)\( \displaystyle + \small \left.\dfrac{N-1-Npn+pn}{N-1}\right) \)
\( \displaystyle \phantom{V(X)} = \small np\left(\dfrac{-pN-n + N +pn}{N-1}\right) \)
\( \displaystyle \phantom{V(X)} = \small np\left(\dfrac{(1-p)(N-n)}{N-1}\right) \)
Finalement, nous obtenons :
\( \displaystyle V(X) = np(1-p)\dfrac{N-n}{N-1} \)

