Vecteurs

Géométrie
 | Lundi 22 Septembre 2025

Les vecteurs sont les éléments servant à caractériser les déplacements, c'est à dire les transformations que l'on appelle des translations.

1. Notion de vecteur

Définition : un vecteur consiste en la donnée :
  1. d'une droite, appelée direction du vecteur.
  2. d'un sens sur cette droite.
  3. d'une longueur, appelée norme du vecteur.

Exemple : considérons deux points \( A \) et \( B \). Alors le vecteur \( \overrightarrow{AB} \) a pour :
- direction : la droite \( (AB) \).
- sens : de \( A \) vers \( B \).
- norme : la longueur \( AB \).

Définitions :
  1. deux vecteurs sont colinéaires s'ils ont des directions parallèles.
  2. deux vecteurs sont égaux s'ils ont des directions parallèles, le même sens et de même normes.
  3. deux vecteurs sont opposés s'ils ont des directions parallèles, des sens différents et de même normes.

Remarque - Des vecteurs égaux sont donc colinéaires.
De même, des vecteurs opposés sont colinéaires.

Exemple : considérons deux points \( A \) et \( B \).
Alors le vecteur \( \overrightarrow{AB} \) est l'opposé du vecteur \( \overrightarrow{BA} \).

Attention !
Que se passe-t-il si on souhaite caractériser une translation allant de \( A \) en \( A \) ?
Il n'y a pas de mouvement ! On définit ainsi le vecteur nul, noté \( \vec{0} \).
S'il n'a pas de direction, pas de sens, il a tout de même une norme : 0.

2. Multiplier les vecteurs

Définition : considérons un vecteur \( \overrightarrow{AB} \) et un nombre réel \( k \neq 0 \).
Alors \( k\times\overrightarrow{AB} \) est un vecteur ayant :
  1. une direction : une droite parallèle à \( (AB) \).
  2. un sens : de \( A \) vers \( B \) si \( k \) est positif, et de \( B \) vers \( A \) si \( k \) est négatif.
  3. une norme : \( k\times AB \).

Exemple : considérons un segment \( [AB] \) et son milieu \( M \).

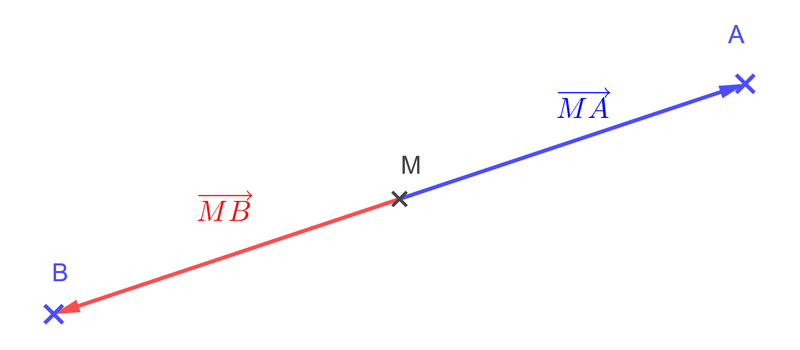
Alors :

\( \overrightarrow{MA} = \dfrac{1}{2} \overrightarrow{BA} \)

\( \overrightarrow{MB} = \dfrac{1}{2} \overrightarrow{AB} \)

\( \overrightarrow{AB} = 2 \overrightarrow{MB} = -2 \overrightarrow{AM} \)

Propriété ! Deux vecteurs \( \vec{u} \) et \( \vec{v} \) sont colinéaires si et seulement si il existe un nombre réel \( k \neq 0 \) tel que \( \vec{u} = k\times\vec{v} \).

Preuve : admis !

3. Additionner les vecteurs

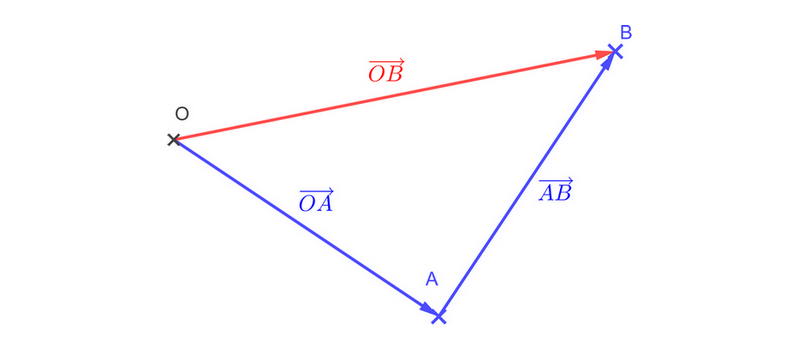
Relation de Chasles : considérons deux vecteurs \( \overrightarrow{AB} \) et \( \overrightarrow{BC} \).
Alors : \( \overrightarrow{AB} + \overrightarrow{BC} = \overrightarrow{AC} \)

Problème !
Considérons deux vecteurs \( \vec{u} \) et \( \vec{v} \). Comment faire pour les additionner ?

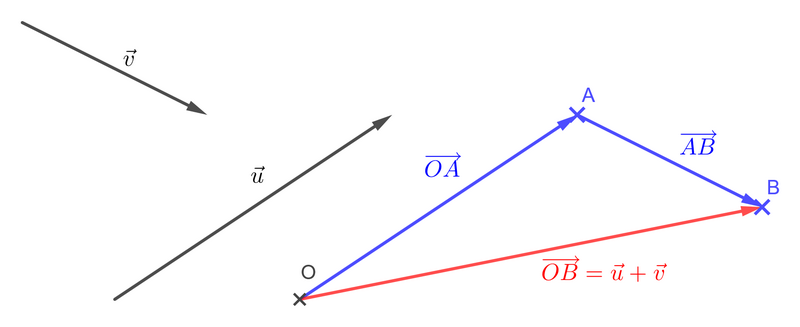
- étape 1 : on place un point \( O \).
- étape 2 : on construit le point \( A \) tel que \( \overrightarrow{OA} = \vec{u} \)
- étape 3 : on construit le point \( B \) tel que \( \overrightarrow{AB} = \vec{v} \).

On a alors, d'après la relation de Chasles :

\( \vec{u} + \vec{v} = \overrightarrow{OA} + \overrightarrow{AB} = \overrightarrow{OB} \).