■

Solution

Rappelons que pour tout entier naturel \( n>0 \), la fonction dérivée de \( x^n \) est \( nx^{n-1} \).

Rappelons aussi que la dérivation est une opération linéaire.

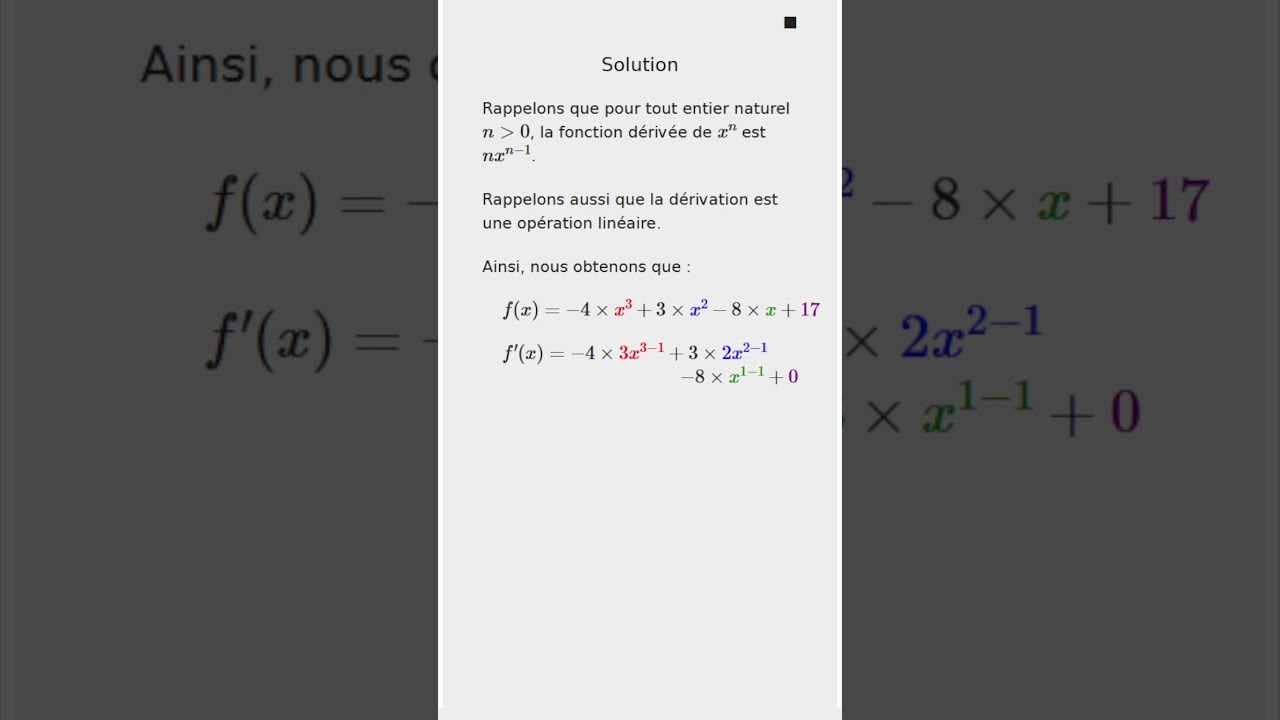
Ainsi, nous obtenons que :

$("#js-6").innerHTML = '\\(' + 'f(x) = ' + op * a + '\\times{\\color{red}x^3} + ' + b + '\\times{\\color{blue}x^2} - ' + c + '\\times{\\color{green}x} + {\\color{purple}' + d + '}\\)';

$("#js-7").innerHTML = '\\(' + 'f\'(x) = ' + op *a + '\\times{\\color{red}3 x^{3 - 1}} + ' + b + '\\times{\\color{blue}2x^{2 - 1}}\\)'; $("#js-8").innerHTML = '\\(' + '-' + c + '\\times{\\color{green}x^{1-1}}+ {\\color{purple} 0}\\)';

$("#js-9").innerHTML = '\\(' + 'f\'(x) = ' + 3*op *a + 'x^2 + ' + 2*b + 'x - ' + c + '\\)';