Objectif
Déterminer l’équation réduite d’une droite à partir des coordonnées de deux de ses points.

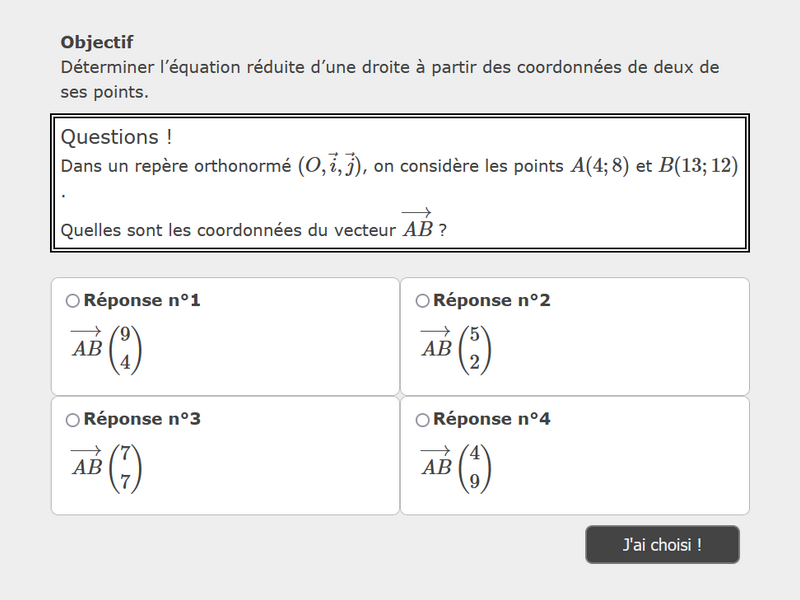
Questions !
Dans un repère orthonormé \( (O, \vec{i}, \vec{j}) \), on considère les points $("#js-1").innerHTML = '\\(' + 'A(' + xA + '; ' + yA + ')\\)'; et $("#js-2").innerHTML = '\\(' + 'B(' + xB + '; ' + yB + ')\\)';.
Quelles sont les coordonnées du vecteur \( \overrightarrow{AB} \) ?

 

Réponse n°1

$("#js-6").innerHTML = '\\(' + '\\overrightarrow{AB} \\begin{pmatrix}' + rand(2, 5) + '\\\\' + rand(6, 9) + '\\end{pmatrix}\\)';

Réponse n°2

$("#js-5").innerHTML = '\\(' + '\\overrightarrow{AB} \\begin{pmatrix}' + rand(2, 5) + '\\\\' + rand(2, 5) + '\\end{pmatrix}\\)';

Réponse n°3

$("#js-4").innerHTML = '\\(' + '\\overrightarrow{AB} \\begin{pmatrix}' + rand(6, 9) + '\\\\' + rand(6, 9) + '\\end{pmatrix}\\)';

Réponse n°4

$("#js-3").innerHTML = '\\(' + '\\overrightarrow{AB} \\begin{pmatrix}' + xu + '\\\\' + yu + '\\end{pmatrix}\\)';

 

 

 

Pour information

Vous n'avez pas encore testé cette question ?!